 Notice. New forum software under development. It's going to miss a few functions and look a bit ugly for a while, but I'm working on it full time now as the old forum was too unstable. Couple days, all good. If you notice any issues, please contact me. |
Forum Index : Microcontroller and PC projects : MMBasic Integers and DDS Arithmetic.
| Author | Message | ||||
| Keith W. Senior Member  Joined: 09/10/2011 Location: AustraliaPosts: 118 |
Hi, I hope for some advice on the best way to handle an MMbasic mathematical process that in past projects have used 40 bit assembler binary arithmetic in a controller CPU. Thebackshed members with amateur radio calls will be familiar with the large frequency numbers and know of DDS but I will explain in some detail that everyone can help. DDS’s are interesting. Likely Tassyjim will have a method to hand already. I have found many methods for assembler but none for Basic. How to do this with MMBasic which does not handle integers to this many bits? Should I synthesize my present process using multiple variables or is there another way? I think MMBasic will handle integers to 24 bits therefore I will not require as many registers/variables as my micro in assembler. My current process requires 28 bit tests, 27 left shifts and possibly 28 additions. There has been discussions on thebackshed regarding integers, has anyone faced a similar problem? The details: - Direct Digital Synthesis is a method for creating any precise frequency at will between wide limits. DDS can be performed in software but not to radio frequencies. There are specialized chips. The chips use a fixed high frequency clock oscillator and are programmed with a 32 bit binary number via a serial interface (SPI). The output is typically a sine wave from an inbuilt A to D converter and Sine ROM table. Once set the output wave will continue without further CPU help until the frequency is changed. Basically DDS requires the repeated addition of a number to a binary accumulator every clock cycle, the most significant bits (14?) of the accumulator address a ROM phase addressed table of a Sine waveform, giving digital values that are converted to an analog voltage by a digital to analog converter. It is possible to use DDS techniques with the Micromite to generate low to medium frequencies, with an external A to D converter or by summing digital outputs with resistors. The waveform could be Sine or anything else repetitive from a table. It is possible to use less than the 32 to 48 accumulator bits detailed here.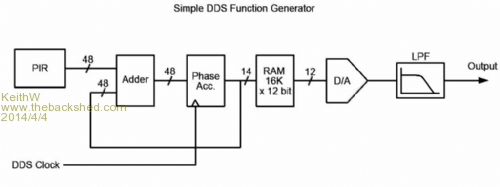 
Think of the 16K* 12 bit Ram as the ROM sine lookup table in this borrowed block diagram. The PIR register holds the factor needed to generate the required output frequency. If the PIR, adder, and phase accumulator support 48-bit additions, then the fractional frequency resolution is one part in 2^47, or about 1 × 10^14. This provides better than 1 Micro-Hz resolution on a 10 MHz output. It is possible to purchase an assembled small circuit board with a 32 bit AD9850 DDS with 10 bit A to D c/w oscillator and filter capable of up to about 60 MHz sine output from $12 MiniKits (or EBay $7.80). A DDS can also generate usable output to very low frequencies if the circuit external to the DDS will allow. 
A few years ago I built myself an RF Generator using an Analog Devices AD9954 chip that with a 100 MHz crystal clock generates a sine output anywhere between 10 KHz and 100 MHz to about 0.1 Hz accuracy. The AD9954 contains a 14 bit digital to analog converter and ROM to generate the sine output with low distortion. My generator is self contained, but under control of a PC program GUI can sweep and plot frequency response over an 80 dB level range using a logarithmic power head, works very well. To calculate the control word ‘M’ to load into the DDS. M = F * 2^N/ C Where F = desired frequency N = number of bits in the accumulator C = DDS clock frequency Because N and C are constant, M may be found for other frequencies subsequently by scaling, it need only be calculated once for a system. For my generator: - 134,217,728 Hz {Magic Frequency}* 4,294,976,296 {2^32} / 400,000,000 {100 MHZ crystal * 4 in DDS} = 1,441,151,880.76 or 55E63B88 Hex {M} by my calculator, correctly 55E63B89. The Magic frequency is 8000000 Hex, which number makes the rest of the calculations simpler. Therefore In my generator the seed factor is 55E63B89 Hex, which is the control word (M) required for frequency 8000000 Hex. That it happens to be actually 134,217,728 Hz is not important. Note that just the 28th bit is set in this hex frequency and it is greater than half my highest desired output frequency. This enables me to conveniently perform the calculation for other output frequencies by addition only. Progressively testing each bit of the required output frequency (in binary) and, if set, adding to the result register(s). The process starts by testing the 28th (the most significant) binary bit of the required frequency and, if set, 55E63B89 is added to the control word. Next divide this seed by 2 (shifting it all right 1 bit) and test the 27Th frequency bit and if set add this divided seed to the control word. Next divide the seed again. Follow this process for all the possible 28 bits of the desired frequency. Then transmit the summed up control word to the DDS. Due to the repeated additions and left shifts I use 40 bit registers to effectively give fractions to preserve accuracy, and then use the whole bits of the result. This bit testing, adding and shifting is performing in binary to 32 bit accuracy the calculation: - New M = Old M * New Frequency / Old Frequency, where Old M and Old frequency are predetermined constants. The control word at least must be converted to Hex for transmission to the DDS and the numbers when calculating must be to about 40 bits The low cost DDS board plus a Micromite entice me towards a simple and inexpensive but precise Audio Oscillator which can be extended for other experiments. I hope others are now excited about DDS. There is a lot of information about DDS on the web. Keith W. |
||||
| JohnS Guru  Joined: 18/11/2011 Location: United KingdomPosts: 3816 |
If MMBasic will be fast enough and all you need is (say) 40 bits max, I think 2 variables will do. May as well store 20 bits in each. You just have to implement the (arithmetic/etc) operators you need. There's a library already I think that does big integer or the like maths but it will be quite slow and do far more than you need, probably. Much easier and faster to do from C (or ASM) so I suppose an alternative is ask Geoff for the source and tweak it. John |
||||
| robert.rozee Guru Joined: 31/12/2012 Location: New ZealandPosts: 2350 |
depending upon the application and the stability of your crystal, you may be able to simplify the task quite a bit. my first observation is that 400,000,000MHz is divisible by 1024, so your multiplier becomes (2^22)/390625. both numbers are representable exactly as integers in micromite basic (which handles integers up to a bit over +/- 16 million). the next question is how stable your crystal is. the precision of micromite reals is around 8 digits, or 1 part in 100,000,000. it seems that most consumer crystals will fall far short of this, and it is relatively pointless being able to set a frequency any more precisely than the likely drift one will see in the crystal over an average room temperature range (probably 15 to 25 degrees C is a fair estimate for temperatures that will be seen in a lab). bottom line, i'd suggest using standard 4-byte reals. you then just need to write a short function that converts the control word, M, from a real into hex digits by repeated division by 16, accepting that your value of M will still be far better than the crystal stability warrants. rob :-) |
||||
TassyJim Guru Joined: 07/08/2011 Location: AustraliaPosts: 6102 |
An interesting project. I have ordered a module to play with ($5.94 posted) and downloaded the data sheets. By the time it arrives, I might have the current projects out of the way. The big integer program I wrote (a few years ago) was to prove that it could be done. Provided you keep the big numbers as strings, just about anything can be done. Strings are limited to 255 characters so that should be good enough resolution! Jim VK7JH MMedit  MMBasic Help |
||||
Grogster Admin Group  Joined: 31/12/2012 Location: New ZealandPosts: 9308 |
A fascinating thread. I don't have anything useful to add here, but I will be watching this thread with interest. Smoke makes things work. When the smoke gets out, it stops! |
||||
| Keith W. Senior Member Joined: 09/10/2011 Location: AustraliaPosts: 118 |
Thank you for the replies, and seems like I do have TassyJim interested. Rob and John have brought me back to earth a bit and are of course correct about why such high precision? I guess that I was looking for a general answer for all cases. For an audio oscillator M could be more than satisfied by MMbasic integer and then zero the more sig bits of M. 1 part in 10^5 would be more than sufficient. You have given me a kick start to experiment with MMBasic for this; my old brain needs help in blowing out the cobwebs and learning how to do things. Rob, as you raise oscillator precision… I had become captured by timing precision, working upon a GPS referenced frequency source to lock my home brew frequency meter. But its reference is now a pre-loved DTCXO (Digital processing Temperature Compensated Crystal Oscillator) which is rated to 1 part in 10^7 accuracy over an extended temperature variation. It is better in practice over a limited temperature range and good enough for practical purposes. But the DTCXO seems to have slight background wander/jumps so not for better precision. I think due to the “digital” control but excellent otherwise for temperature stability. I now have a pre-loved Rubidium Standard source with a 10 MHZ output (accuracy parts in 10^10), that is how I found out about the limitation of the DTCXO’s. Modern technique seems to be to lock a Rubidium (good short term) to GPS (better long term). Can achieve parts in 10^13. The Atomic Clocks in GPS satellites are corrected from the ground for long term drift but due to transmissions jitters not so good short term. Picosecond jitters in the 1 PPs pulse. You have to integrate correction for possibly days. As a New Zealander, Rob could type “ZL1BU Frequency Reference” into Google. There are many interesting things to discover and think about. When working I did not have the time. Keith W |
||||
| paceman Guru Joined: 07/10/2011 Location: AustraliaPosts: 1329 |
"Wired" magazine had an interesting write-up last week on the very new NIST F2 cesium standard that's just been authorised. Apparently it's three times more accurate than the current NIST F1 standard and accurate to a second in 300 million years - I reckon that would do the job Keith. Check it out: New global cesium standard. Greg |
||||
jwettroth Regular Member  Joined: 02/08/2011 Location: United StatesPosts: 71 |
I think I would use strings to store some kind of hex strings. If you packed it, you could store a 40 bit number in length 5 bytes- but I would probably use unpacked for simplicity and use length 10 strings. Floating point can really make a mess of things if what you're after is big integers. You could write a few functions to handle these invented numbers strings. I think it's the easiest way to go. I am a ham (KF4EUZ) and have played quite a bit with DDS's from ADI (the 9851 mainly and the lower freq 9834's). Great parts. Good Luck. John Wettroth |
||||
 Print this page |
